|
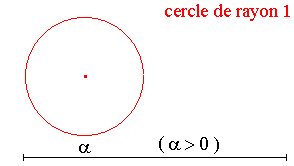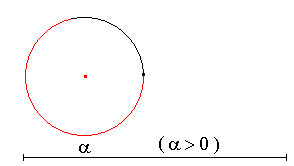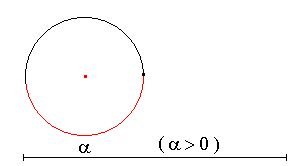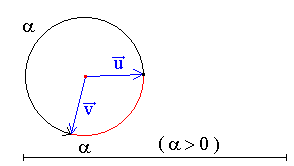
On peut définir un angle de vecteur pour deux vecteurs 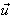 et
et 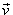 quelconques de l'espace
ou du plan , il suffit de prendre deux représentants de quelconques de l'espace
ou du plan , il suffit de prendre deux représentants de 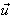 et
et 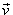 de même origine. de même origine.
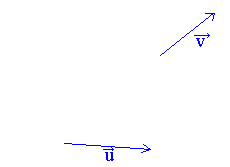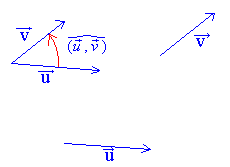
Mesures d'un angle orienté
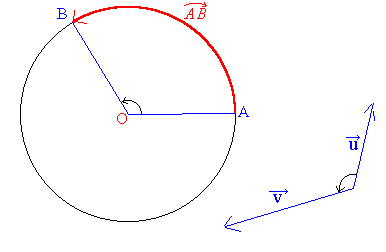
On appelle mesure de l'angle orienté  toute mesure de l'arc orienté
intercepté par cet angle.
toute mesure de l'arc orienté
intercepté par cet angle.
Soient A, B deux points d'un cercle de centre O , on dit que l' arc 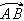 orienté intercepte l'angle
orienté intercepte l'angle
 si si 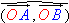 =
=  . .
Réciproquement : à un nombre réel 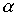 correspond un unique angle orienté
correspond un unique angle orienté 
( 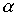 est positif dans
l'exemple ) est positif dans
l'exemple )
Rappel sens positif = sens inverse des aiguilles d'une montre jusqu'à
présent
Si le nombre 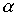 est
une mesure de l'angle est
une mesure de l'angle
 il existe une infinité
de mesure de l'angle, tout nombre réel de la forme il existe une infinité
de mesure de l'angle, tout nombre réel de la forme 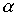 + k2
+ k2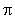 ou k ou k 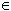 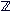 est une mesure de l'angle
est une mesure de l'angle  . .
la mesure particulière de l'angle  appartenant à l'intervalle ]-
appartenant à l'intervalle ]- 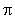 ; ;
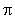 ] est appelé mesure
principale de l'angle ] est appelé mesure
principale de l'angle  . .
Propriétés
pour tous vecteurs 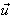 ,
, 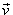 et et 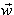 non nuls on a :
non nuls on a :
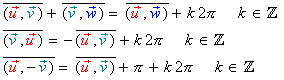
on note 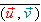 une mesure
de l'angle de vecteur une mesure
de l'angle de vecteur  ou bien mes
ou bien mes
|

 Glossaire
Glossaire Bibliographie
Bibliographie Calendrier
Calendrier Liens
Liens Aide
Aide