Définition 1 : On appelle barycentre
des points A et B ( ou A et B deux points du plan ou de l'espace )
affectés respectivement des coefficients 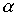 ,
, 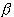 ( ou ( ou
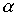 ,
, 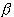 sont des réels tels que
sont des réels tels que 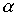 +
+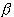 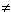 0 l'unique point G tel que
0 l'unique point G tel que 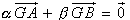 (1) (1)
Définition 2 : On appelle barycentre
des points A et B ( ou A et B deux points du plan ou de l'espace)
affectés respectivement des coefficients 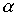 ,
, 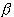 ( ou ( ou
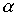 , , 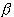 sont des réels tels que
sont des réels tels que 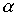 +
+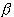 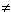 0) l'unique point G tel que pour tout point M du plan ou de l'espace
on a : (
0) l'unique point G tel que pour tout point M du plan ou de l'espace
on a : (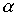 +
+ 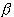 ) ) 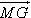 =
= 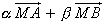 (2) (2)
Pour placer le point G, on peut prendre M = A d'où : 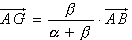
Remarque : A, G, B sont alignés.
Cas particulier : si les coefficients
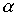 et
et 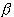 sont
égaux et non nuls le barycentre G des points A
et B affectés respectivement des coefficients sont
égaux et non nuls le barycentre G des points A
et B affectés respectivement des coefficients 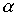 ,
, 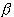 est le
milieu du segment [AB]. L' isobarycentre de 2 points A et B est donc le
milieu du segment [AB]. est le
milieu du segment [AB]. L' isobarycentre de 2 points A et B est donc le
milieu du segment [AB]. |
Définition 1 : Dans le
plan ou dans l'espace , le barycentre G de 3 points A, B, C affectés des
coefficients 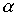 ,
, 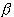 , , 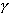
(avec 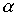 +
+ 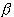 + + 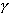 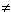 0 ) est le point unique tel que :
0 ) est le point unique tel que :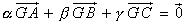
Définition 2 : Dans le plan ou dans l'espace , le barycentre
G de 3 points A, B, C affectés des coefficients 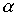 ,
, 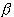 , ,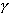
(avec 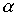 + + 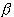 + +
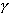 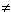 0 ) est le point unique tel que pour tout point M on a :
0 ) est le point unique tel que pour tout point M on a :
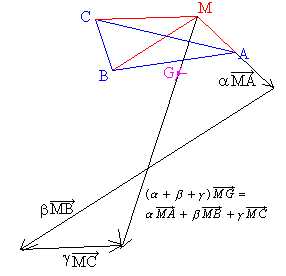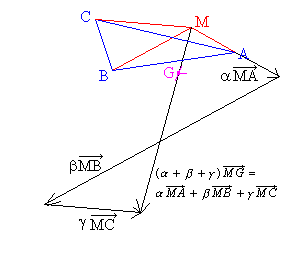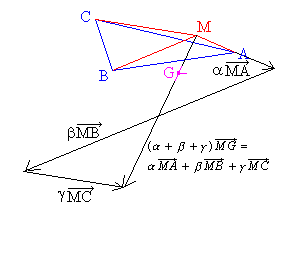
(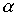 + + 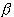 + +
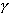 ) ) 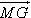 =
= 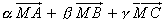 
Les définitions 1 et 2 sont équivalentes :
- en effet en prenant M = G on retrouve l'égalité
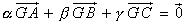 (2)
donc définition 2 (2)
donc définition 2 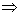 définition 1
définition 1
- En faisant intervenir M dans l'égalité (2) on retrouve
la égalité de la définition 2 donc définition 1
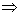 définition 2.
définition 2.
|

 Glossaire
Glossaire Bibliographie
Bibliographie Calendrier
Calendrier Liens
Liens Aide
Aide