|
Théorème du barycentre partiel :
On ne change pas le barycentre de n points lorsqu'on remplace
p ( p < n )
de ces points par leur barycentre affectés de la somme des coefficients
des p points considérés.
Remarques : cette propriété permet de ramener toute
construction de barycentre de plusieurs points à la construction
d'un barycentre de 2 points.
On peut très bien se servir de cette propriété
en sens inverse : c'est à dire que l'on peut très bien
remplacer un point par un ensemble de points pondérés.
Pour comprendre d'où vient cette propriété :
prenons l'exemple par défaut de cette page :
G est le barycentre de A(3),B(2),C(4),D(-3),E(9)
donc on a :
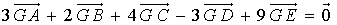 (1) (1)
considérons alors le point H barycentre
de A(3),B(2),C(4) on
a :
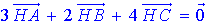 (2)
(2)
Faisons intervenir le point H dans
(1)
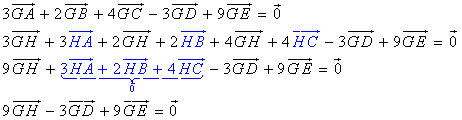
On en déduit G barycentre de H(9), D(-3) et G(9)
|

 Glossaire
Glossaire Bibliographie
Bibliographie Calendrier
Calendrier Liens
Liens Aide
Aide