|
Caractérisation des
homothéties- translations :
Pour qu'une transformation f soit une homothétie-translation, il faut et il suffit qu'il existe
un réel k non nul tel que pour tous points M et N d'images respectives M'
et N'
Remarque : si k = 1 , f est une translation;
si k 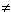 1, f est une homothétie. 1, f est une homothétie.
L'ensemble des homothéties munie de la loi o des
compositions des applications est un groupe :
- le produit commutatif ( la composée ) de deux translations de vecteurs
respectifs 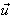 et et 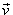 est une translation de vecteur
est une translation de vecteur 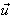 et
et 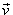 donc une dilatation. donc une dilatation.
-le produit de deux homothéties de rapport k et k' est soit une
translation, soit une homothétie.
-le produit d'une homothétie de rapport k par une translation de vecteur 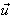 est encore une homothétie.
est encore une homothétie. |

 Glossaire
Glossaire Bibliographie
Bibliographie Calenderier
Calenderier Liens
Liens Aide
Aide