Glossaire>

Distance

La distance est une application qui à tout couple
(A; B ) de points du plan ou de l'espace fait correspondre un réel positif, noté AB, et qui possède les propriétés suivantes :

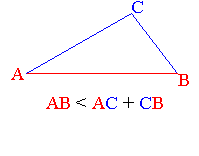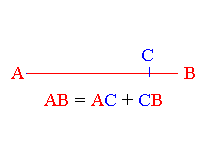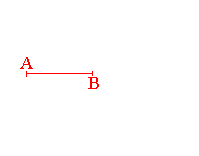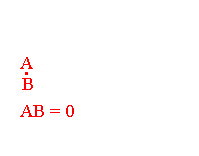
• quels que soient les points A, B, C du plan ou de l'espace : AB AC + CB ( inégalité triangulaire )
• quels que soient les points A et B :
  AB = 0 si et seulement si A = B
• AB = BA
  

Caractérisation d'un segment [AB] avec la distance

le segment [AB] est l'ensemble des points M du plan ( ou de l'espace )
tels que AB = AM + MB

Caractérisation d'une droite (AB) avec la distance

la droite (AB) est la réunion des trois ensembles de points suivants :

• ensemble des points M du plan ou de l'espace tels que AB = AM + MB
• ensemble des points M du plan ou de l'espace tels que AM = AB + BM
• ensemble des points M du plan ou de l'espace tels que BM = BA + AM

Milieu d'un segment [AB]

On appelle milieu du segment [AB], l'unique point I de [AB] tel que AI = IB si A et B sont distincts et I = A = B si A et B sont confondus.