Glossaire>

Groupes (quelques notions)

Définition de groupe :
Un ensemble G muni d'une loi est un groupe si :

• est une loi de composition interne sur G
• La loi est associative.
• admet un élément neutre dans G
• Tout élément x de G admet un symétrique x' dans G

Dans le cas ou est commutative, on dit que (G, ) est un groupe commutatif.

Exemple : (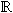, + ) est un groupe commutatif. (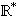, x) est un groupe.

Définition de sous groupe :
On dit que H est un sous groupe de G, si H est une partie non vide de G et H est un groupe muni de la même loi de composition interne de G.

Le théorème suivant permet de montrer qu'un sous ensemble H est un sous groupe d'un groupe de G :
Soit (G, ) un groupe , ou x' représente l'élément symétrique de x.
Si H est un sous ensemble non vide de G tel que pour tout élément x de H et tout élément y de on a : x y' appartient à H, alors H est un sous groupe de G.

Groupes isomorphes : deux groupes (F, +) et (G, * ) sont isomorphes, si il existe un isomorphisme entre F et G.