Glossaire>

Isométries du plan

Les isométries du plan sont les applications du plan vers lui-même, qui conservent les distances, on distingue 2 types d'isométries :

• les déplacements ou isométries positives
  ( résultat d'un glissement du plan sur lui-même) , les seuls déplacements plan sont 
  la rotation, la translation, l'identité du plan
  
• les antidéplacements ou isométries négatives.
  (glissement du plan composé avec un retournement du plan ) sur lui même )
  
  un antidéplacement dans le plan est soit une réflexiond'axe une droite ( appelée aussi symétrie orthogonale ) ou une composée d'une réflexion du plan et d'une translation (symétrie glissée )

L'ensemble (I ; o) des isométries du plan muni de la loi de composition o est un groupe puisque c'est un sous groupe des transformations du plan :

• I n'est pas vide puisque id_P 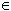I.
• la composée de deux isométries est encore une isométrie.
  Preuve : soient f et g deux isométries du plan, soient A et B deux points quelconque du plan, tels que A'=f(A) , B'=f(B), A''=f(A'), B''=f(B')
  alors AB = A'B' et A'B' = A''B'' donc AB = A''B'' donc g o f est encore une isométrie.