Glossaire>

Lieux géométriques dans le plan

Comment définir un lieu géométrique ?
Dans ce type de problème , il s'agit de déterminer l'ensembles des positions occupées par un point variable , lié par des propriétés géométriques à certains éléments d'une figure ( éléments fixes )
Quelques exemples de lieu géométriques classiques :

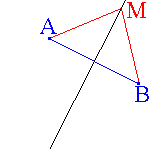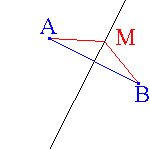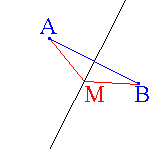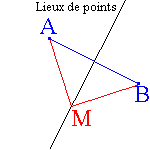
• dans le plan , si on considère deux points A et B de ce plan distincts l'ensemble des points M du plan 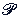tels que les vecteurs 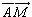et 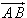est la droite (AB) (caractérisation vectorielle d'une droite )

• dans le plan ,si on considère deux points A et B de ce plan distincts, l'ensemble des points M du plan barycentres des points A et B est la droite (AB)

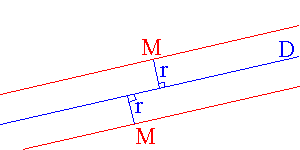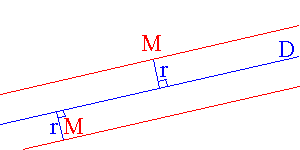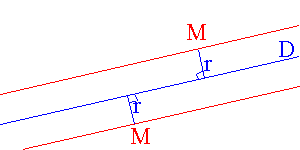
• dans le plan ,si on considère une droite D et un réel strictement positif r , l'ensemble des points M du plan
  tel que la distance de M à la droite D est r est la réunion de deux droites parallèles à D
  

• dans le plan 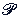, si on considère deux droites D et D' sécantes l'ensemble des points M du plan équidistants des droites D et D' est la réunion des deux bissectrices de (D, D')
  
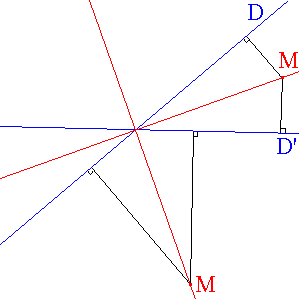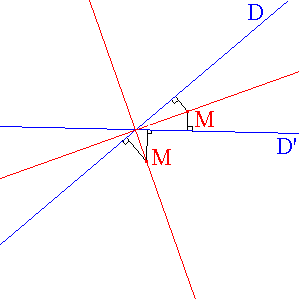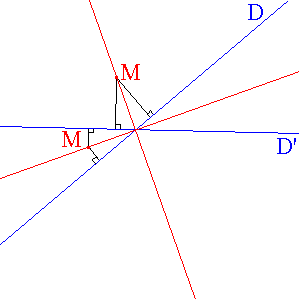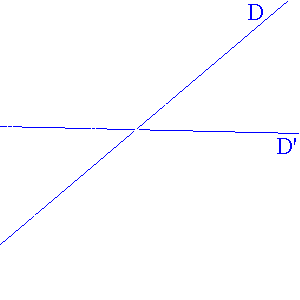
  ( si D et D' sont parallèles on trouve la parallèle commune à D et D' qui est équidistante des deux droites )
  

• dans le plan , si on considère deux points A et B distincts et 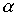un réel , l'ensemble des points M du plan tel que :
  -
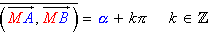
  est le cercle passant par A et B ( A et B exclus ) tangent en A à la droite (AT) définie par ((AT),(AB)) = 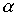+ k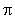
  -
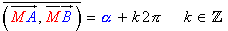
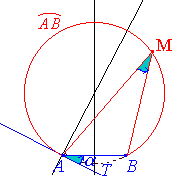
  est l'un des arcs de cercle ( A et B exclus )