Glossaire>

Théorème de Ménélaus

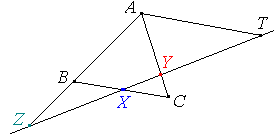
Soient ABC un triangle, et X, Y, Z trois points pris respectivement sur les côtés (BC), (CA), (AB), pour que les points X, Y, Z soient alignés il faut et il suffit que :


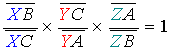
Démonstration :

1. Montrons que si X, Y, Z sont alignés alors :
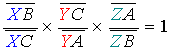
   en appliquant le théorème de Thalès dans le triangle ATZ et le triangle ATY , on a :
   
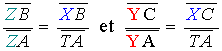
   on en déduit l'égalité :
   
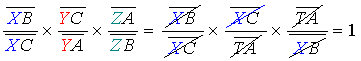
2. Montrons que si X, Y, Z vérifient
   
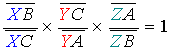
   alors X, Y, Z sont alignés :
   démontrons tout d'abord que la droite (YZ) ne peut que couper la droite (BC)
   supposons que la droite (YZ) soit parallèle à la droite (BC) alors d'après le théorème deThalès appliqué dans le triangle ABC on a :
   
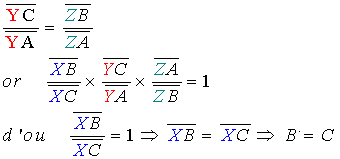
   ce qui est impossible donc la droite (YZ) coupe la droite (BC) , soit X' le point d'intersection des deux droites on a d'après 1) :
   
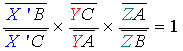
   or
   
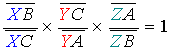
   donc
   
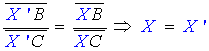
   donc X, Y, Z alignés