Glossaire>

Similitude plane directe

Une similitude du plan est une application du plan conservant les rapports de distances pour tous les couples de points et leurs images.
Une similitude directe de rapport k >0 est une transformation du plan qui multiplie les distances par k, et conserve les angles orientés .

Une similitude directe est une application du plan vers lui même composée d'une homothétie et d'un déplacement (ou l'inverse )

En fait toute similitude directe ( autre qu'une translation) peut être considérée comme composée d'une rotation et d'une homothétie de même centre I ( ou inversement) dans ce cas on dit similitude de centre I de rapport k > 0  ( rapport de l'homothétie ) et d'angle a ( angle de la rotation).

- toute homothétie plane de rapport k< 0 est une similitude de rapport |k| et d'angle p .
- toute isométrie positive est une similitude de rapport 1 ( et réciproquement )
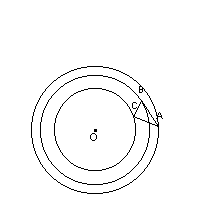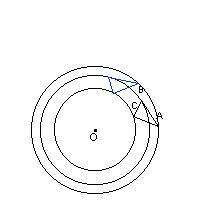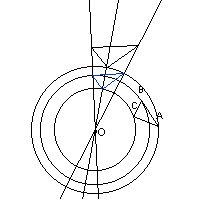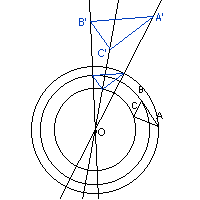
- l'image d'un cercle C(O;R) par une similitude est un cercle C(O' ; R) ou O' est l'image de O par la similitude.
- une similitude directe étant le produit de 2 applications affines ( elle conserve les barycentres ) est une application affine.

Théorème : l'ensemble des similitudes directes du plan muni de la loi o est un groupe.