Isométrie 1 > Rotation > Définition

Soit 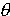un réel et O un point du plan .
La rotation de centre O et d'angle 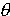est une isométrie du plan : c'est la transformation du plan qui à tout point M du plan associe le point M' tel que :

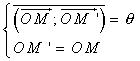
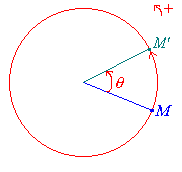
En fait, le point M' appartient au cercle de centre O et de rayon OM et l'angle 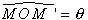dans le sens impliqué par le signe de :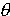
- si 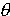< 0 , la rotation se fait dans le sens, dit sens indirect ou négatif , c'est à dire le sens des aiguilles d'une montre,
- si 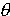>0, la rotation se fait dans le sens, dit sens direct ou positif , c'est à dire le sens des aiguilles d'une montre.
Ce qui explique l'utilisation d'angle de vecteur pour définir une rotation.

Cas particuliers : 
- une rotation d'angle plat ou d'angle de mesure p radians est une symétrie centrale (dans le plan)
- une rotation d'angle droit ou d'angle de mesure p/2 radians est appelée quart de tour direct
- une rotation d'angle nul est l'identité du plan