On considère deux rotations r1 et r2 de
centres respectifs O1 et O2, et d'angle respectif
de mesure 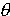 1 et 1 et
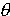 2 , la composée de
ces deux rotations peut être suivant les cas une rotation d'angle
d'angle 2 , la composée de
ces deux rotations peut être suivant les cas une rotation d'angle
d'angle 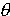 1 + 1 +
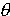 2 ou bien une
translation. 2 ou bien une
translation.

démonstration, on décompose les deux rotations en composée de symétrie
axiale. Si on pose  1
et 1
et  2, les droites
passant respectivement par O1 et O2 sont telles
que : 2, les droites
passant respectivement par O1 et O2 sont telles
que :
mes ( (O1O2),
 1) = - 1) = -
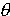 1 /2 et mes ( (O1
O2), 1 /2 et mes ( (O1
O2),  2)
= 2)
= 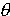 2 /2 2 /2
posons S1 , S2 et S les réflexions d'axes
respectifs (O1O2),
 1, 1,
 2 2
r2 o r1 = (S2 o S )o( S o S1)
= S2 o (S o S ) o S1 = S2 o S1
on a de plus mes (  1
, 1
,  2) = 2) =
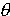 1 /2 + 1 /2 +
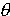 2 /2 = ( 2 /2 = (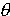 1
+ 1
+ 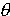 2 )/2 2 )/2
- Cette composée est une translation si les
droites
 1 et 1 et
 2 sont
parallèles quand 2 sont
parallèles quand 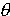 1
+ 1
+ 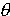 2 = k2 2 = k2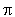 avec k
avec k 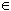
- Cette composée est une rotation de centre
 le point
d'intersection de le point
d'intersection de  1
et 1
et  2 si 2 si
 1 et 1 et
 2 sont
sécantes, l'angle de cette rotation est 2 sont
sécantes, l'angle de cette rotation est
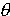 1 + 1 +
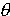 2 2
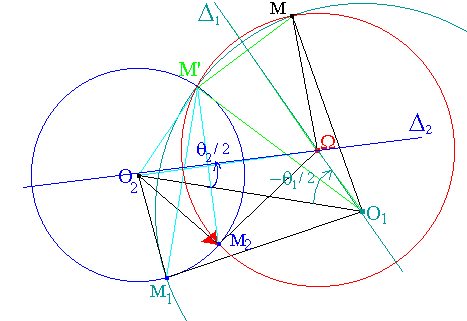
|

 Glossaire
Glossaire Bibliographie
Bibliographie Calendrier
Calendrier Liens
Liens Aide
Aide