- M’ = SD(M) et O
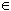 D, donc OM = OM’ D, donc OM = OM’
M’’ = SD’(M’) et O 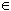 D’, donc OM’’ =OM’ D’, donc OM’’ =OM’
Donc OM = OM’’
D’autre part
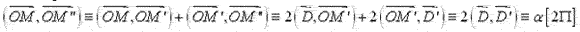
- Pour montrer que deux applications sont identiques il suffit de montrer que l’image d’un point quelconque M est le même par les deux applications
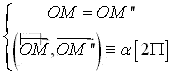 donc r(M) = M’’.
D’autre part on a : SD’ ° SD(M) = SD’(M’) = M’’ donc r(M) = M’’.
D’autre part on a : SD’ ° SD(M) = SD’(M’) = M’’
Par suite r = SD’ ° SD
- Conclusion : Toute rotation de centre O et d’angle
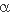 peut être obtenue en composant deux symétries orthogonales dont les axes se coupent en O et font entre eux un angle égal à peut être obtenue en composant deux symétries orthogonales dont les axes se coupent en O et font entre eux un angle égal à 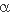 /2 (mod /2 (mod 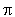 ), le choix du premier axe étant arbitraire. ), le choix du premier axe étant arbitraire.
|

 Glossaire
Glossaire Bibliographie
Bibliographie Calendrier
Calendrier Liens
Liens Aide
Aide