Isométrie 1 > Rotation > Propriétés

- La rotation d’angle nul est l’identité du plan.

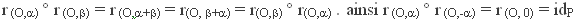donc toute rotation est une bijection du plan sur lui-même, et l’inverse de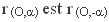

- Soit r la rotation de centre O et d’angle 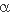. Notons A’ = r (A), et B’ = r (B) alors A’B’ = AB. Ainsi toute rotation du plan est une isométrie du plan.

- L’image d’un segment (respectivement, une droite, une demi droite, un cercle, un angle, etc) par une rotation est un segment (respectivement, une droite, une demi droite, un cercle, un angle, etc).

- Si l’angle d’une rotation de centre O est non nul, alors O est le seul point fixe de cette rotation. En fait un point M est fixe si et seulement si M = O

- Toute rotation de centre O laisse invariant tout cercle centré en O

- Toute rotation conserve les angles orientés