|
Quelques pistes pour prouver l'alignement de 3 points A, B, C :
- montrer que les vecteurs
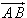 et
et 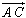 sont colinéaires. sont colinéaires.
- montrer que les droites (AB) et (AC) sont confondues
- montrer que l'angle
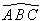 est
nul ou plat. est
nul ou plat.
- montrer que les points A, B, C appartiennent à certain ensemble
de points ( médiatrice, bissectrice etc...)
- montrer que A, B, C sont les images de 3 points alignés par
une application qui conserve
l'alignement.
- appliquer le théorème
de Ménélaüs
- montrer que C est l'image de B par une
homothétie de centre A
- montrer que A, B, C sont tels que AB = AC + CB ( ou AC = AB + BC ou
BC = BA + AC, voir distance
)
Quelques pistes pour prouver que 3 droites D1, D2,
D3 sont concourantes :
|

 Glossaire
Glossaire Bibliographie
Bibliographie Calendrier
Calendrier Liens
Liens Aide
Aide